
Per introdurre l’argomento, oggi partiremo da una definizione:
la definizione di fattore K
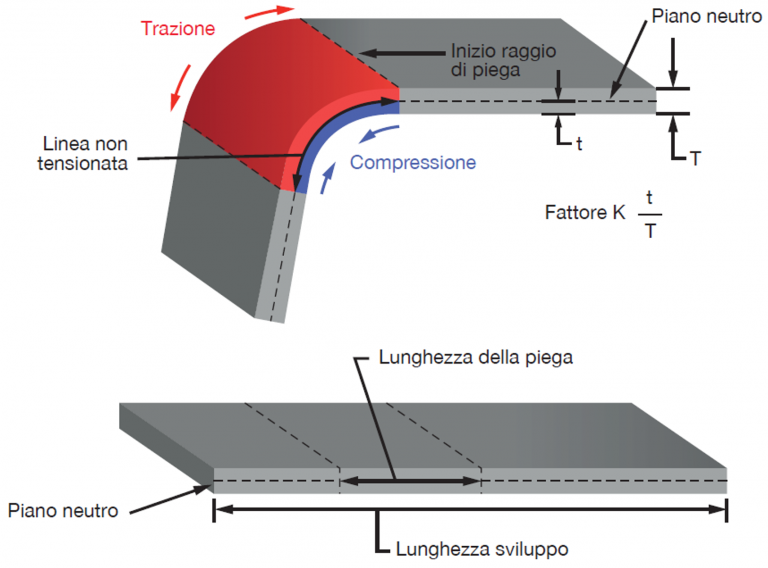
Si, e il piano neutro cosa è?
Semplice, è quel sottile strato ideale in cui le fibre del metallo non subiscono tensioni di trazione o di compressione e va da sé che quella zona ideale non subisce variazioni di lunghezza: non si accorcia, né si allunga.
Ora, nonostante la formula teorica che serve a determinare il fattore K (che comunque merita di essere capita) possiamo tranquillamente affermare che nelle condizioni più frequenti, quindi con raggi interni pari o inferiori allo spessore (es: spessore 30/10- r 2,5 o 3 mm) vale la semplificazione che vuole il piano neutro a circa un terzo dello spessore partendo dall’interno.
Perché proprio lì?
Perché per come è fatto l’acciaio è più facile “stirarlo che comprimerlo”.
Alcune carpenterie hanno individuato il fattore K a 5/12 anziché a 1/3, ma non c’è un abisso di differenza!
Tuttavia ricordiamo che per spessori elevati tende a spostarsi verso il centro, così come con gli acciai altoresistenziali.
Ma soffermiamoci alla formula teorica per la determinazione del fattore K.
ATTENZIONE!
Questa formula molto diffusa non dà come risultato il fattore K, ma il suo doppio!
Infatti, nella formula per trovare il tratto deformato di uno sviluppo, deve essere diviso per 2.
Dunque:
K(doppio)=log(ri/s)x0,5+0.65
Dove log è LOGARITMO IN BASE 10, ri è il raggio interno, s è lo spessore.
E lì il piegatore Franco (collega di Osvaldo) si dice: “Ma che ca… è il logaritmo in base 10?!“
Franco ha ragione: il logaritmo in base 10 è una funzione matematica, una specie di inverso della potenza, ad esempio log in base 10 di 100 è 2.
Senza farci troppe domande sappiamo che sulla carta ha un grafico come quello in questa seguente figura.
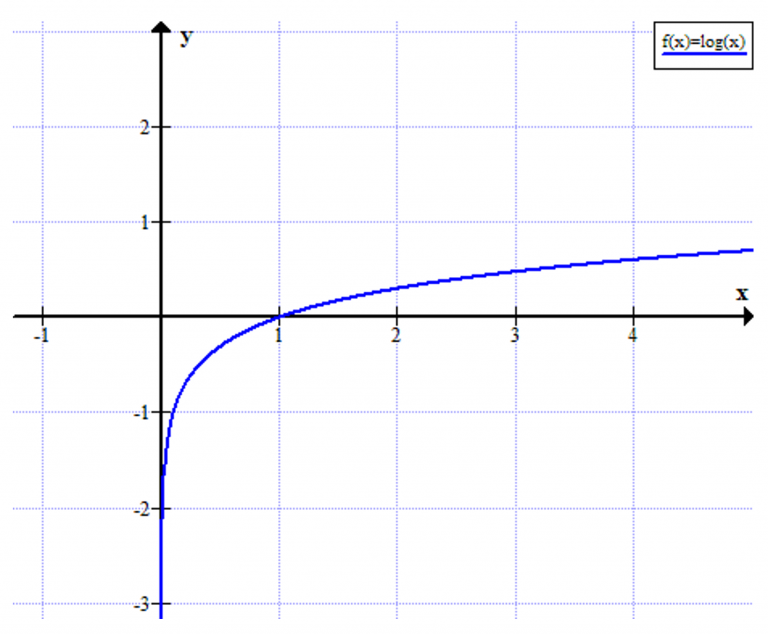
Come ci sono arrivati i pazzi che hanno redatto questa formula?
Beh, empiricamente, credo, ma ne sono piuttosto sicuro.
Ossia, facendo decine e decine di prove, hanno messo su un grafico una nuvola di punti di rilevazione e quella nuvola ha la forma della curva della funzione del logaritmo in base 10 ed ecco fatto: tradotto in matematica un comportamento fisico.
Ma torniamo alla nostra formula per trovare il fattore K con un esempio:
Ho un 30/10 da piegare in matrice V=20
Il raggio interno che ne esce è pari a 2,5mm
Quindi:
log (2.5/3)x0,5+0.65 = prendere la calcolatrice scientifica e fare: 2.5/3 e premere log
Esce -0.07918124 etc.
Da lì in poi è un gioco:
-0.07918124×0.5+0.65 = 0.61 che è il doppio del fattore K del nostro materiale.
Quanto fa 0.61/2? 0.305.
E il fattore K è circa un terzo dello spessore? SI!
K=t/T = 1/3 = 0,3333
Ed ecco qua il collegamento tra teoria e pratica.
Poi tutti gli operatori accorti sanno che la lamiera non è mai uguale a sé stessa e che, dal momento che c’è già abbastanza a cui pensare, ogni semplificazione è grasso che cola.
Aggiungo, in ogni caso, che ognuno ha il suo metodo di riferimento, misure interne o esterne che siano, ma l’importante è capire che ciò che si sta facendo non è frutto della magia e che il proprio non è il metodo unico e infallibile al mondo (a maggior ragione se il risultato è lo stesso di quello degli altri).
ACQUISTA SUBITO LA TUA COPIA!
Clicca ora sulla copertina per riceverla.
E se vuoi saperne di più per migliorare l’attendibilità dei disegni e se ti servono tutti i trucchi che rendono già in fase di disegno la piegatura della lamiera un lavoro molto più snello, puoi fare ben 5 cose:
Scrivermi una mail all’indirizzo emiliano@accademiadellapiegatura.it
Visitare il sito internet www.accademiadellapiegatura.it
Lasciare il tuo Mi Piace alla pagina Facebook di AdP
Diventare un mio collegamento su LinkedIn
Iscriverti al canale YouTbe


